Published: Jan 8, 2020 by Dev-hwon
What is Data Exploration
- 데이터 특성을 더 잘 이해하기 위한 데이터의 예비 탐색
- 전처리 or 분석을 위한 올바른 도구 선택 지원
- 패턴 인식
1. Frequency and mode
- Frequency(빈도수): attribute value의 빈도는 데이터 세트에서 값이 발생하는 횟수(시간)의 백분율
- Mode(최빈수): attribute의 mode는 가장 빈번하게 나오는 attribute values
- frequency와 mode는 주로 categorical data에 사용된다.
2. Percentiles
- 크기가 있는 값들로 이루어진 자료를 순서대로 나열했을 때 백분율로 나타낸 특정 위치의 값
- 일반적으로 크기가 작은 것부터 나열하여 가장 작은 것을 0, 가장 큰 것을 100으로 한다.
- 100개의 값을 가진 어떤 자료의 20 백분위수는 그 자료의 값들 중 20번째로 작은 값을 뜻한다. 50 백분위수는 중앙값과 같다.
3. Measures of Location
- Mean(평균):
- 데이터의 중앙을 대표하는 통계 값
- outliers에 민감하다. \(\bar{x}={\sum_{i=1}^N x_i \over N}\) or \(\bar{x}={\sum_{i=1}^N w_ix_i \over \sum_{i=1}^N w_i}\)
- Median(중위수): * 숫자를 크기에 따라 정렬하였을 때 가장 중앙(50%)에 위치한 값
\(median(x)=\left\{\begin{matrix} x_{(r+1)} && \textbf{if} \: m \: \textbf{is odd, i.e,} \: m=2r+1\\ {1 \over 2}(x_{(r)}+x_{(r+1)}) && \textbf{if} \: m \: \textbf{is even, i.e,} \: m=2r \end{matrix}\right.\)
4. Measures of Spread
- Range: 최대값과 최소값의 차이
- Midrange: 최대값과 최소값의 평균
- variance(분산): 데이터가 평균으로 부처 얼마나 떨어져서 분포하는지 산포를 알아보기 위한 기술량 \(variance(x) = s^2_{x}={1\over{m-1}}\sum_{i=1}^m(x_i-\bar{x})^2\)
- outliers에 민감하기 때문에 다음과 같은 방법을 사용하기도 한다.
\(AAD(x)={1 \over m}\sum_{i=1}^m \left |x_i-\bar{x} \right |\)
\(MAD(x)=median( \left \{ {\left | x_1-\bar{x} \right |} \right \},..., \left \{ {\left | x_m-\bar{x} \right |} \right \})\)
\(IQR\)(interquartile range)는 밑에 설명
5. IQR(interquartile range)
- 4분위수는 분포의 중심, 확산 및 모양을 나타낸다.
- 중간에 50% 데이터들이 흩어진 정도
\(IQR=Q_3-Q_1\)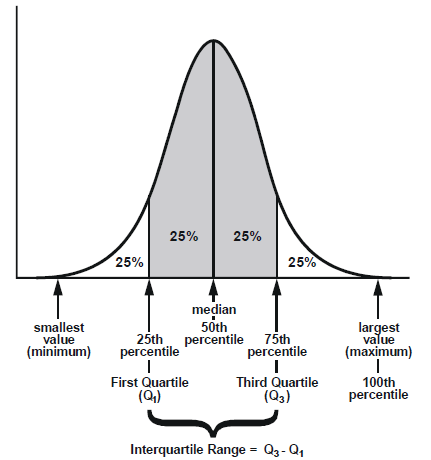
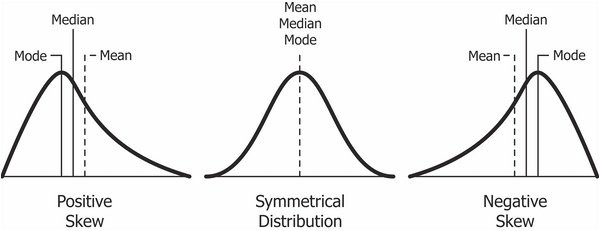
6. Skewness(왜도, 비대칭도)
- 실수 값 확률 변수의 확률분포 비대칭성을 나타내는 지표
- Skewed 되어있는 값을 그대로 학습시키면 꼬리 부분이 상대적으로 적고 멀어서 모델에 영향이 거의 없이 학습. 따라서 변환 필요
\(\gamma_1=E\left [ ({ {X-\mu}\over\sigma })^3 \right ]={E\left [ (X-\mu)^3\right]\over (E \left [ (X-\mu)^2\right ])^{3\over2}}\)
\(\textbf{표본 왜도}:\mathbf{g}_1= { {1 \over n}\sum_{i=1}^n (x_i-\bar{x})^3 \over ({1 \over n}\sum_{i=1}^n (x_i-\bar{x})^2)^{3\over2} }\)
\(\textbf{모 왜도}:\mathbf{G}_1={\sqrt{n(n-1)} \over n-2}g_1\)
7. Kurtosis(첨도)
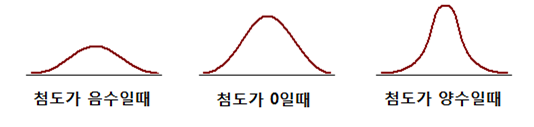
- 자료의 분포가 뾰족한 정도를 나타내는 척도
- 정규분포를 따른다면 첨도값은 0, 중간이 뾰족하다면 첨도값은 0보다 크고, 반대로 중간이 평평하다면 첨도값은 0보다 작은 값
\(\gamma_1=E\left [ ({X-\mu}^4)\over\sigma\right]-3={E\left [ (X-\mu)^4\right]\over (E\left[ (X-\mu)^2\right])^2}-3\)
\(\textbf{표본 첨도}: \mathbf{g}_2=\)\({1\over n}\sum_{i=1}^n (x_i-\bar{x})^4 \over ({1\over n}\sum_{i=1}^n(x_i-\bar{x})^2)^2-3\)
\(\textbf{모 첨도}: \mathbf{G}_2={n-1 \over (n-2)(n-3)}((n+1)g_2+6)\)
8. Coefficent of variation(변동계수, CV)
- 서로 다른 두 집단의 자료분포를 평균 관점에서 어느 정도 퍼져 있나를 대략적으로 확인
- 자료의 평균이 0이거나 0에 가까울 때는 변동 계수가 무한히 커질 수 있기 때문에 주의 할 것
\(CV={\sigma \over \mu}\)
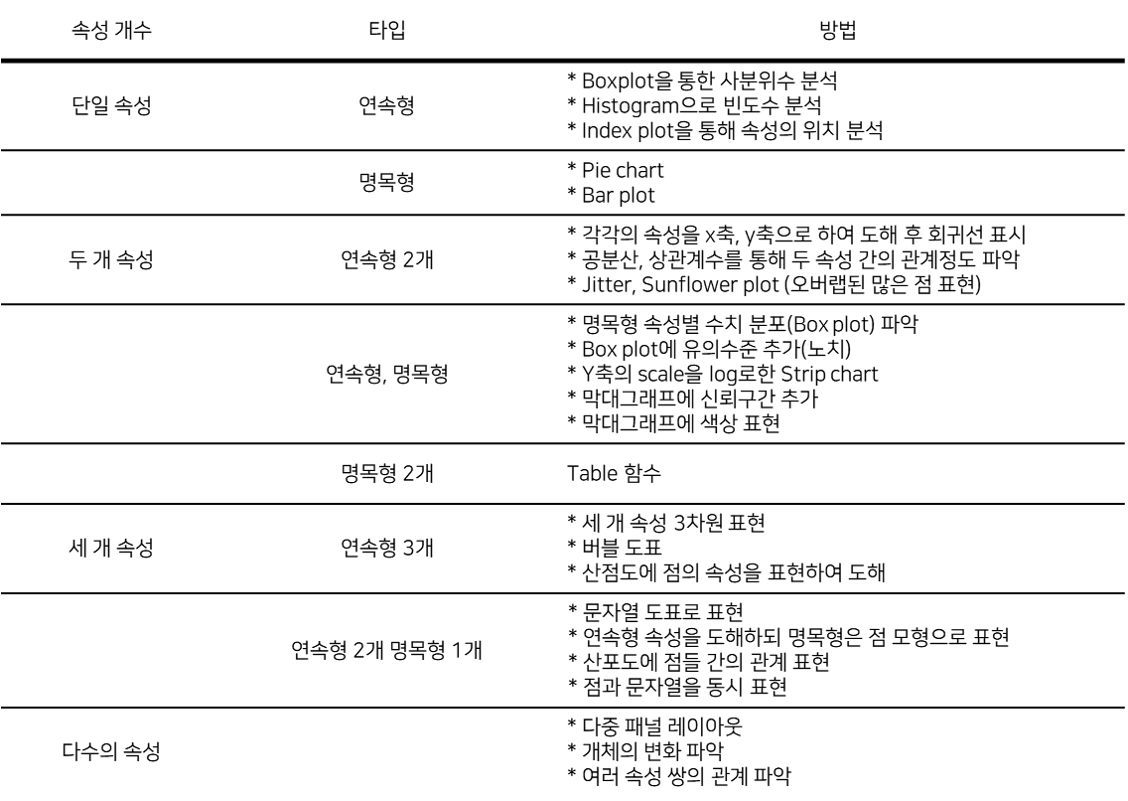
Visualization
- 시각화는 데이터를 시각적 또는 표 형식으로 변환
- 데이터의 특성
- 데이터 항목 또는 속성간의 관계
- 일반적인 패턴과 추세를 감지 할 수 있다.
- outliers 및 특이한 패턴을 감지 할 수 있다.
| 데이터 타입 | 속성 타입 | 기법 |
|---|---|---|
| Record data | Continuous | Histogram, Box plot, Scatter plot (representation) |
| Discrete | Pie chart, Mosaic plot (Contingency table) | |
| Transaction | Network structure (Confusion matrix) |
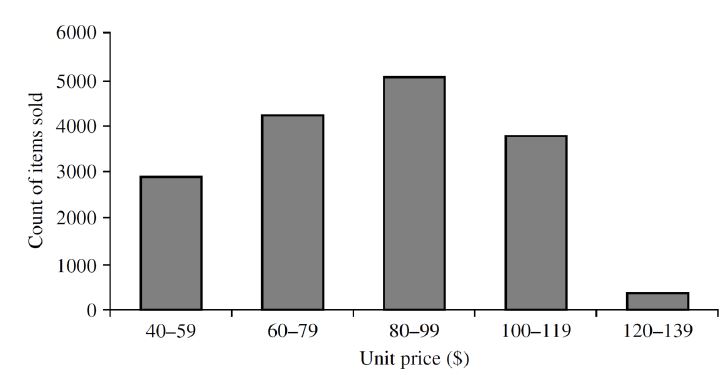
1.Histogram(히스토그램)
- 일반적으로 단일 변수 값의 분포를 보여준다.
- 하위 범위는 버킷 또는 빈이라고 하며 범위는 폭이라고 한다. 일반적으로 버킷의 폭은 동일하다.
- 높이 = 개체 수
- 그룹을 비교하기에는 좋지 않다
- Two-Dimensional Histogram: 두 속성 값의 공동 분포를 보여준다.
!
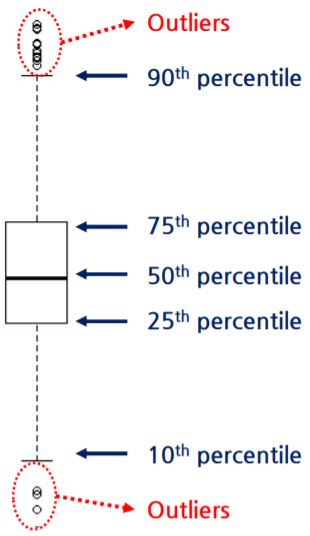
2. Box Plots
- 데이터의 분포를 나타내는 방법
- \(outlier<Q_1-1.5*IQR\) & \(Q_3+1.5*IQR<outlier\)
- attribute들 비교할 때도 사용
- classification 작업에 유용한 attribute를 식별하는데에도 사용
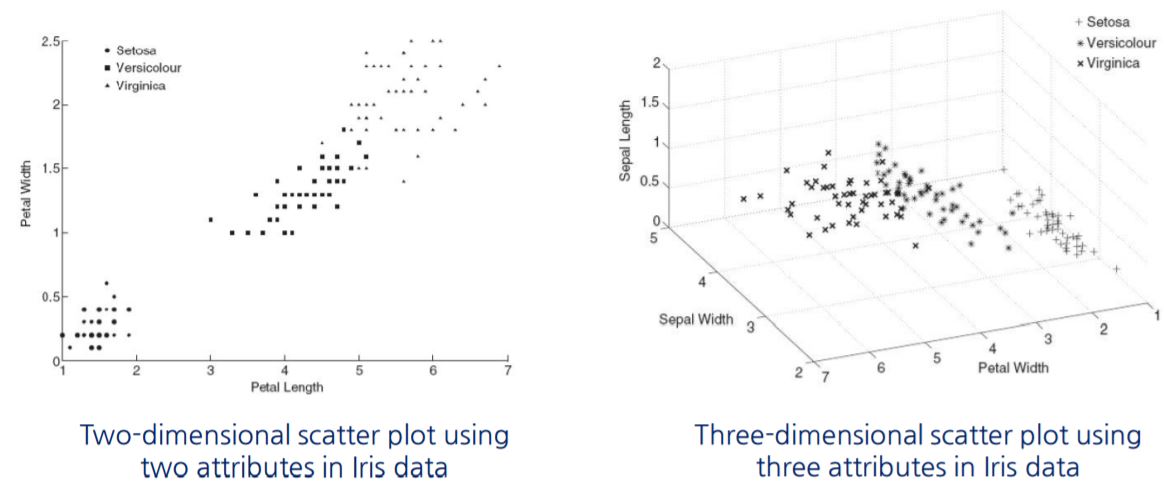
3. Scatter Plots
- 두 가지 numeric attributes 사이의 관계, 패턴 또는 추세를 감지하는 효과적인 방법
- 2차원 scatter plots이 보통 사용되지만 3차원 scatter plots도 사용
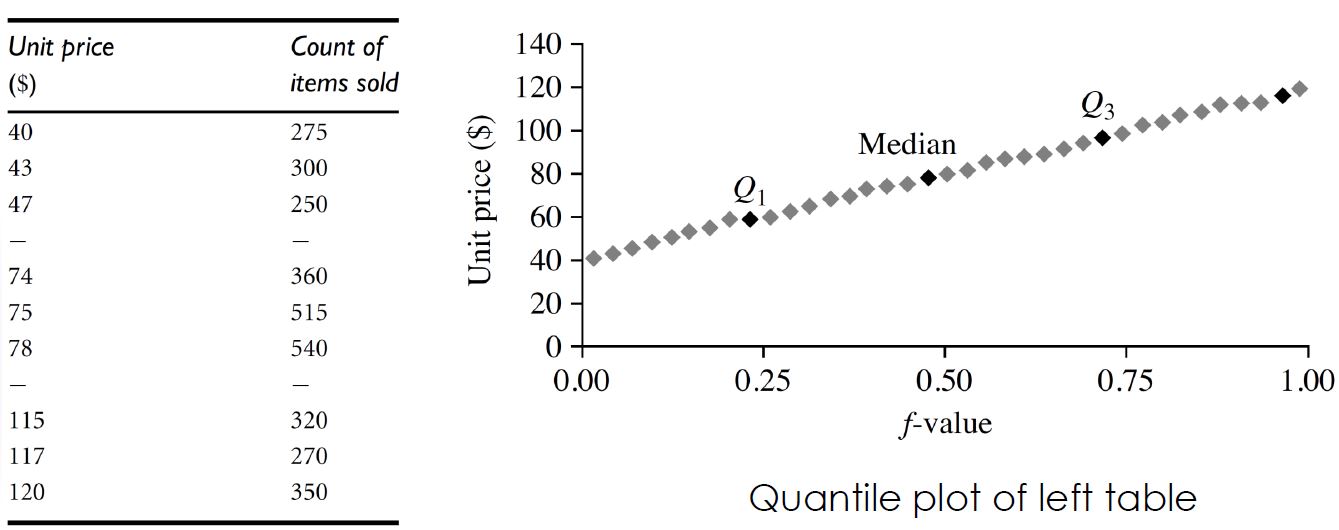
4. Quantile plots
- quantil plots은 단변량 데이터 분포를 먼저 살펴 보는 좋은 방법
- 수집 데이터를 표준 정규 분포의 분위수와 비교하여 그리는 그래프
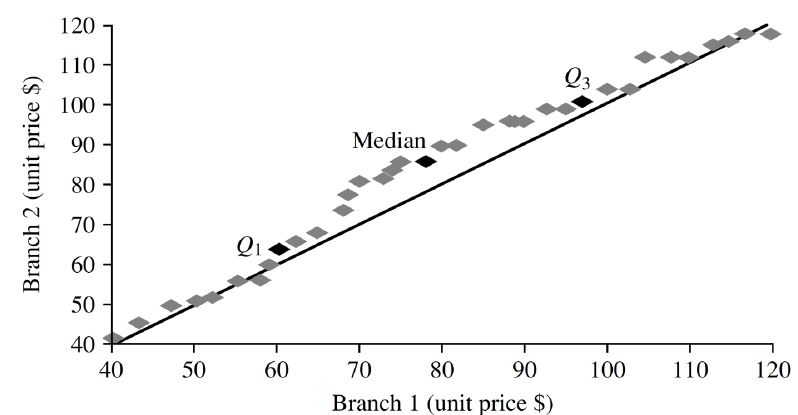
5. Q-Q plots
- 두 확률 분포를 각각의 quantiles를 그려 넣음으로써 비교하는 것
- 두 분포가 비슷하면 y=x 라인
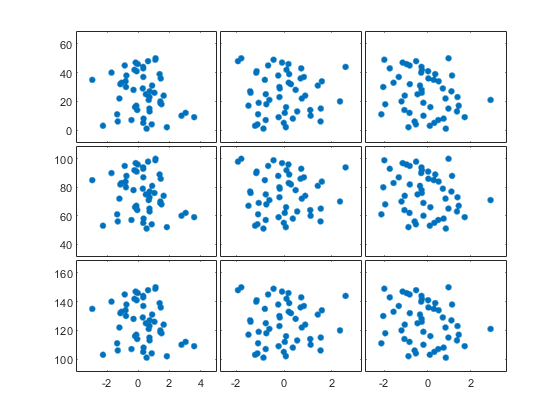
6. Matrix of Scatter plots
- 산점도의 배열이 여러 쌍의 속성의 관계를 간결하게 요약
- 속성이 많을 수록 비 효과적
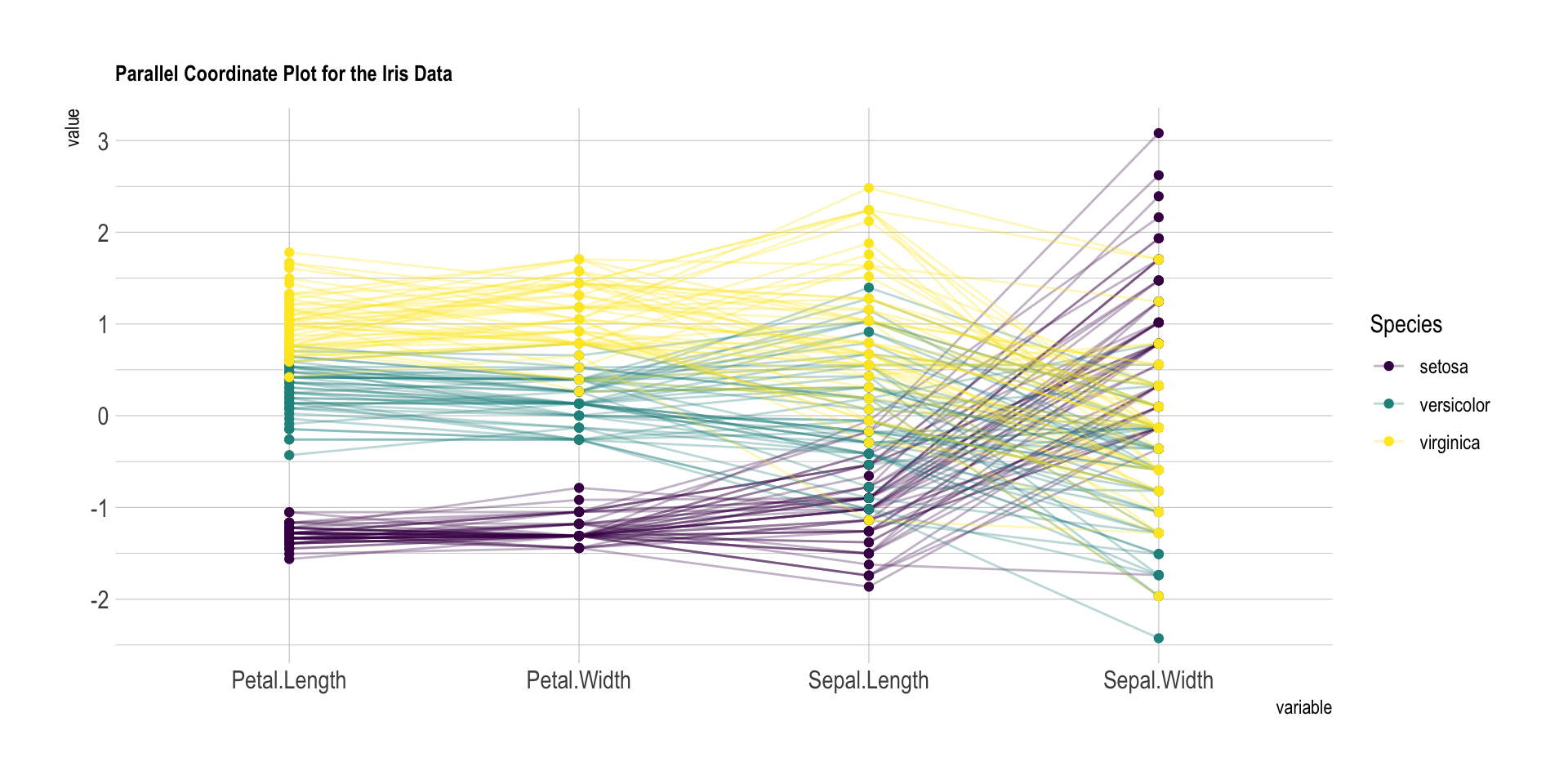
7. Parallel Coordinates
- 평행 좌표를 사용하여 속성이 많은 경우 속성 값을 플로팅 가능
- 각 객체의 속성 값은 각 해당 좌표 축에 점으로 표시되며 점은 선으로 연결
8. Pie chart
- 원형 차트에서 슬라이스 크기는 각 범주의 빈도를 나타낸다.
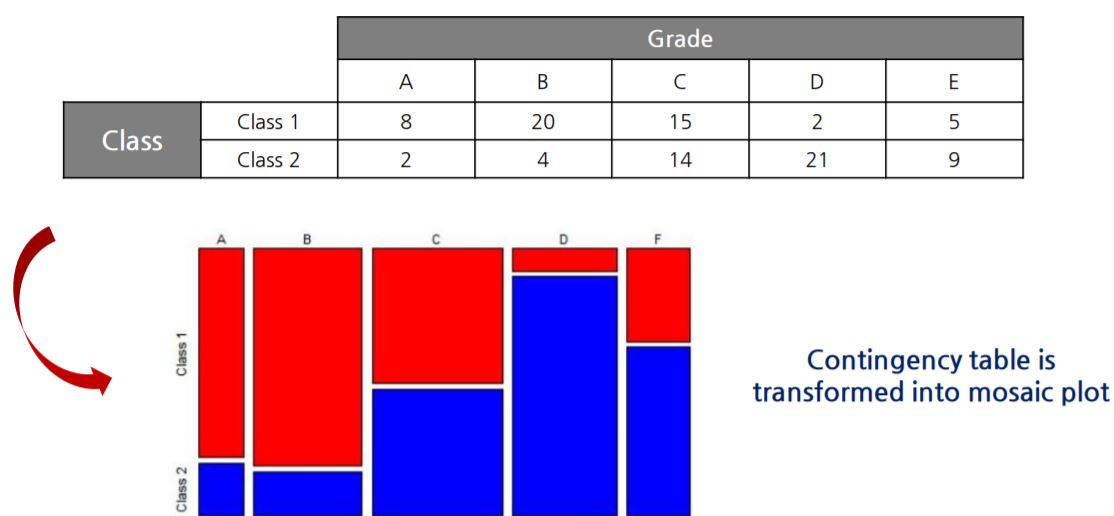
9. Mosaic plots
- 모자이크 플롯은 두 개의 개별 속성 사이의 Contingency table을 기반으로 한다.
- 범주 내 높이는 클래스 내 범주의 상대 빈도수를 나타냅니다.
- 상자 그림과 유사하게 모자이크 그림을 사용하여 분류에 중요한 속성을 식별 할 수 있다.
10. Network structure
- transaction records를 시각화하려면 모든 레코드를 품목간에 confusion matrix로 변환해야한다.
- 그런 다음 confusion matrix는 소셜 네트워크 구조로 표현 될 수 있다.
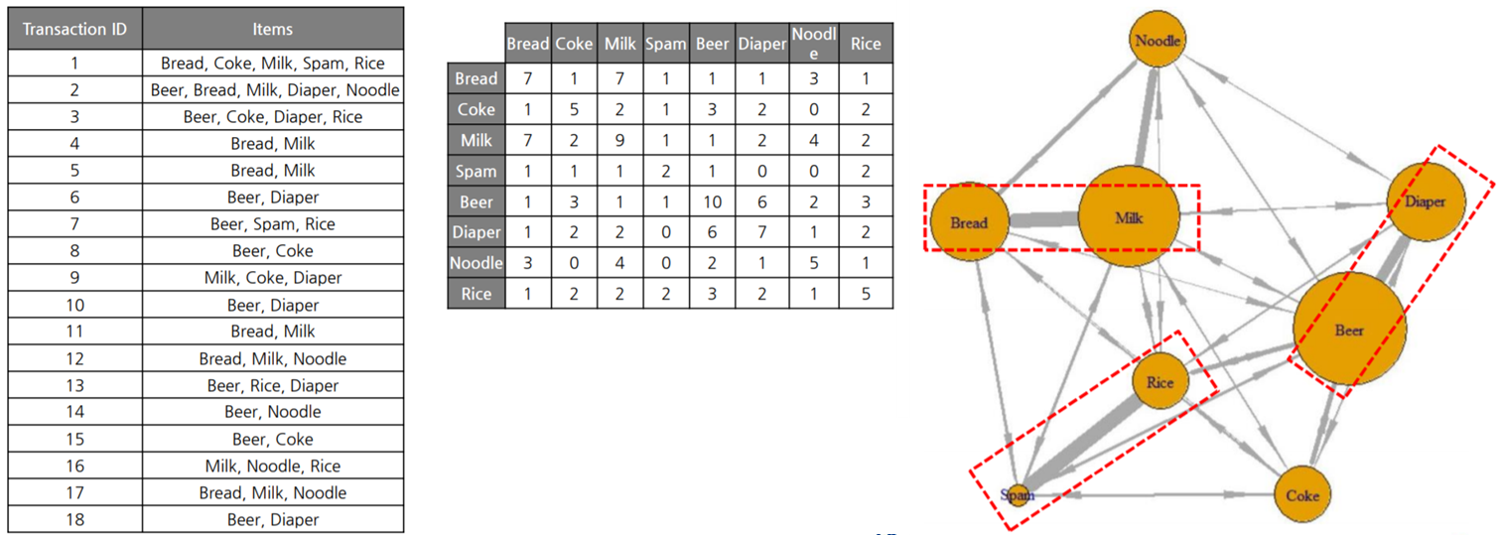
데이터 특성에 따른 분포 조사